Tema: Se analiza el poder decisional de los países de la Unión Europea, con respecto a la regla de votación incluida en el Tratado de la Constitución Europea, aprobado en Bruselas.
Resumen: En la cumbre de Bruselas, celebrada el 18 de junio de 2004, los Jefes de Estado y de Gobierno de la Unión Europea aprobaron la siguiente modificación del texto de la Constitución Europea: “Una mayoría cualificada se definirá como al menos el 55% de los miembros del Consejo, incluyendo al menos a quince de ellos y representando a Estados miembros que tengan al menos el 65% de la población de la Unión. Una minoría de bloqueo debe incluir al menos cuatro miembros del Consejo”. En este análisis se exponen los porcentajes de poder de Banzhaf de los países de la Unión (25 en la actualidad y 27 cuando se incorporen Bulgaria y Rumania) con las reglas de votación de Niza, de la Convención Europea y de la cumbre de Bruselas. Además, se estudia el poder decisional de cada ciudadano europeo con el modelo de Penrose.
Análisis: Los juegos de votación ponderada son modelos matemáticos que se usan para analizar la distribución del poder de decisión de una nación en el seno de una organización supranacional como el Consejo de Ministros de la Unión Europea, el Consejo de Seguridad de las Naciones Unidas o el Fondo Monetario Internacional. En estas instituciones, cada nación dispone de un número de votos y una propuesta queda aprobada si una coalición de naciones suma los votos suficientes para superar una cuota establecida. Por ejemplo, el método de votación del Consejo de Seguridad de las Naciones Unidas, formado por cinco miembros permanentes y diez temporales, es el juego en el que cada una de las naciones permanentes (EEUU, Rusia, China, el Reino Unido y Francia) dispone de siete votos y cada una de las temporales de un único voto, siendo la cuota a superar de 39 votos. Observemos que cualquier coalición que no incluya a alguna nación de las cinco permanentes tiene a lo sumo (4×7)+10 votos, número inferior a la cuota fijada en 39; por lo que no podrá ser una coalición ganadora. Entonces, los miembros permanentes tienen capacidad para vetar cualquier propuesta.
El análisis de las coaliciones decisivas en las que participa cada nación, permite asignarle un índice de poder, que es una medida de su capacidad para lograr coaliciones que superen la cuota adoptada para aprobar decisiones. Es decir, el poder de decisión de una nación se mide calculando el número de veces que sus votos convierten a una coalición que no alcanzaba la cuota en una coalición ganadora. El índice de poder más utilizado fue propuesto por Banzhaf (1965) y proporciona una medida mucho más precisa del poder de un jugador que el número de votos que tiene derecho a emitir. Otra cuestión que se plantea en la toma de decisiones es la siguiente: ¿Cómo se mide el poder de una nación para bloquear una decisión? La respuesta a esta cuestión es que el poder de una nación para bloquear decisiones es el mismo que tiene para aprobarlas. Más precisamente, si las abstenciones no se tienen en cuenta, el índice de Banzhaf mide tanto la capacidad de una nación para aprobar una propuesta como para bloquearla (véase Dubey y Shapley, 1979).
El método de votación aprobado en la cumbre de Bruselas el 18 de junio de 2004, para su incorporación a la Constitución Europea, es más complejo porque se basa en un sistema de doble votación. Para aprobar una propuesta en el Consejo de Ministros de la Unión Europea, se necesitan al menos 15 países que reúnan más del 65% de la población. Además, el número mínimo de países para bloquear una propuesta se establece en cuatro y las abstenciones no se contabilizan. El grupo de investigación de Teoría de Juegos de la Universidad de Sevilla, del que soy responsable, ha desarrollado un nuevo método combinatorio para calcular el número de coaliciones decisivas en juegos con votaciones dobles (véanse las referencias bibliográficas 1, 3, 4 y 5).
En el escenario de 25 países miembros de la Unión Europea, se pueden formar 33.554.431 de coaliciones no vacías. Las coaliciones decisivas que obtienen dichos países en el juego de doble votación y en el juego de bloqueo con al menos cuatro países, se exponen en las columnas segunda y tercera de la Tabla 1. En la cuarta columna, se presenta el número de coaliciones decisivas con la regla aprobada en la cumbre de Bruselas.
Tabla 1. Coaliciones decisivas de los 25 miembros de la Unión Europea
| EU 25 | Doble votación | Bloqueo 4 | Total |
| Alemania | 2.668.027 | 2.668.019 | |
| Francia | 1.940.159 | 0 | 1.940.159 |
| Reino Unido | 1.929.669 | 0 | 1.929.669 |
| Italia | 1.889.319 | +2 | 1.889.321 |
| España | 1.490.413 | +2 | 1.490.415 |
| Polonia | 1.422.169 | +4 | 1.422.173 |
| Países Bajos | 962.829 | +12 | 962.841 |
| Grecia | 851.897 | +12 | 851.909 |
| Portugal | 842.213 | +12 | 842.225 |
| Bélgica | 842.213 | +12 | 842.225 |
| República Checa | 832.527 | +12 | 832.539 |
| Hungría | 832.527 | +12 | 832.539 |
| Suecia | 813.199 | +12 | 813.211 |
| Austria | 793.799 | +12 | 793.811 |
| Dinamarca | 736.231 | +12 | 736.243 |
| Eslovaquia | 736.231 | +12 | 736.243 |
| Finlandia | 726.573 | +12 | 726.585 |
| Irlanda | 707.217 | +12 | 707.229 |
| Lituania | 697.547 | +12 | 697.559 |
| Letonia | 668.999 | +12 | 669.011 |
| Eslovenia | 659.337 | +12 | 659.349 |
| Estonia | 649.681 | +12 | 649.693 |
| Chipre | 640.093 | +12 | 640.105 |
| Luxemburgo | 630.555 | +12 | 630.567 |
| Malta | 630.555 | +12 | 630567 |
Estos datos demuestran que la cláusula de exigir al menos cuatro países para bloquear tiene un impacto insignificante en la distribución del poder. Alemania pierde ocho coaliciones decisivas, Francia y el Reino Unido mantienen las mismas coaliciones decisivas, Italia y España ganan dos y Polonia cuatro. Estas ganancias o pérdidas de los países más poblados se suman o restan a más de un millón de coaliciones. Además, los 19 países con menor población ganan 12 coaliciones decisivas que suman a más de medio millón de dichas coaliciones, que estos países tienen en el juego de doble votación sin la cláusula de bloqueo.
En la Tabla 2 se exponen las coaliciones decisivas de las 25 naciones de la Unión Europea y de las dos naciones candidatas (Rumania y Bulgaria). En este escenario, Alemania también pierde ocho coaliciones decisivas, Francia, el Reino Unido e Italia mantienen las mismas, España y Polonia ganan cuatro; mientras que los 21 países más pequeños ganan 10 coaliciones decisivas. Debemos tener en cuenta que el número de coaliciones no vacías en el escenario de 27 países es 134.217.727 y las coaliciones decisivas oscilan entre 1.824.817 y 13.708.647, correspondientes a Malta y Alemania respectivamente.
Tabla 2. Coaliciones decisivas de los 25 miembros de la Unión Europea y 2 candidatos
| EU 27 | Doble votación | Bloqueo 4 | Total | ||
| Alemania | 13.708.647 | 13.708.639 | |||
| Francia | 10.090.873 | 0 | 10.090.873 | ||
| Reino Unido | 10.039.263 | 0 | 10.039.263 | ||
| Italia | 9.743.561 | 0 | 9.743.561 | ||
| España | 7.362.225 | +4 | 7.362.229 | ||
| Polonia | 6.800.035 | +4 | 6.800.039 | ||
| Rumania | 4.871.079 | +10 | 4.871.089 | ||
| Países Bajos | 4.048.155 | +10 | 4.048.165 | ||
| Grecia | 3.326.413 | +10 | 3.326.423 | ||
| Portugal | 3.237.845 | +10 | 3.237.855 | ||
| Bélgica | 3.231.183 | +10 | 3.231.193 | ||
| República Checa | 3.210.689 | +10 | 3.210.699 | ||
| Hungría | 3.196.981 | +10 | 3.196.991 | ||
| Suecia | 3.033.941 | +10 | 3.033.951 | ||
| Austria | 2.911.521 | +10 | 2.911.531 | ||
| Bulgaria | 2.877.541 | +10 | 2.877.551 | ||
| Dinamarca | 2.530.351 | +10 | 2.530.361 | ||
| Eslovaquia | 2.530.351 | +10 | 2.530.361 | ||
| Finlandia | 2.509.871 | +10 | 2.509.881 | ||
| Irlanda | 2.332.655 | +10 | 2.332.665 | ||
| Lituania | 2.264.209 | +10 | 2.264.219 | ||
| Letonia | 2.099.685 | +10 | 2.099.695 | ||
| Eslovenia | 2.051.511 | +10 | 2.051.521 | ||
| Estonia | 1.962.711 | +10 | 1.962.721 | ||
| Chipre | 1.873.045 | +10 | 1.873.055 | ||
| Luxemburgo | 1.831.725 | +10 | 1.831.735 | ||
| Malta | 1.824.817 | +10 | 1.824.827 | ||
La consecuencia que se desprende de los datos presentados en las Tablas 1 y 2 es que el requisito de exigir al menos cuatro países para bloquear una decisión complica el procedimiento innecesariamente, porque el cambio en la distribución del poder es insignificante.
El índice de Banzhaf de una nación se obtiene dividiendo el número de coaliciones decisivas en las que participa dicha nación por el número total de coaliciones decisivas. Así, se obtiene una distribución, entre cero y uno, de la capacidad de decisión para aprobar mociones en una institución. Si multiplicamos por cien dicho índice, obtenemos el porcentaje de poder de Banzhaf. En la Tabla 3 se exponen los porcentajes de población y de poder de Banzhaf de las 25 naciones de la Unión Europea con la regla de Niza, la regla de la Convención Europea (al menos 13 naciones con más del 60% de la población) y la regla aprobada en la cumbre de Bruselas para incorporarla a la Constitución Europea (al menos 15 naciones con más del 65% de la población, y con más de 4 naciones para bloquear). Los datos de población utilizados para calcular los citados índices son los facilitados por la Oficina del Censo de Eurostat correspondientes al 1 de enero de 2003.
Tabla 3. Poder de Banzhaf de los 25 miembros de la UE con tres reglas de votación
| EU 25 | Población | Niza | 13 & 60% | 15 & 65% & B |
| Alemania | 18,158 | 8,5606 | 13,360 | 10,424 |
| Francia | 13,118 | 8,5600 | 9,4887 | 7,5805 |
| Reino Unido | 13,052 | 8,5600 | 9,4281 | 7,5395 |
| Italia | 12,610 | 8,5600 | 9,1807 | 7,3818 |
| España | 9,141 | 8,1221 | 7,0202 | 5,8233 |
| Polonia | 8,408 | 8,1221 | 6,7677 | 5,5566 |
| Países Bajos | 3,562 | 4,2284 | 3,6395 | 3,7619 |
| Grecia | 2,424 | 3,9103 | 2,9610 | 3,3285 |
| Portugal | 2,290 | 3,9103 | 2,9040 | 3,2907 |
| Bélgica | 2,278 | 3,9103 | 2,9040 | 3,2907 |
| República Checa | 2,245 | 3,9103 | 2,8470 | 3,2528 |
| Hungría | 2,231 | 3,9103 | 2,8470 | 3,2528 |
| Suecia | 1,967 | 3,2725 | 2,7328 | 3,1773 |
| Austria | 1,775 | 3,2725 | 2,6188 | 3,1015 |
| Dinamarca | 1,184 | 2,3102 | 2,2730 | 2,8766 |
| Eslovaquia | 1,183 | 2,3102 | 2,2730 | 2,8766 |
| Finlandia | 1,145 | 2,3102 | 2,2155 | 2,8389 |
| Irlanda | 0,872 | 2,3102 | 2,1002 | 2,7632 |
| Lituania | 0.762 | 2,3102 | 2,0423 | 2,7255 |
| Letonia | 0,513 | 1,3292 | 1,8682 | 2,6139 |
| Eslovenia | 0,439 | 1,3292 | 1,8102 | 2,5762 |
| Estonia | 0,298 | 1,3292 | 1,7523 | 2,5384 |
| Chipre | 0,157 | 1,3292 | 1,6943 | 2,5010 |
| Luxemburgo | 0,099 | 1,3292 | 1,6360 | 2,4637 |
| Malta | 0,087 | 0,9933 | 1,6360 | 2,4637 |
En la Tabla 4 se exponen los porcentajes de población y poder de Banzhaf de las 25 naciones de la Unión Europea y de las dos naciones candidatas (Rumania y Bulgaria) con la regla de Niza, la regla de la Convención Europea (al menos 14 naciones con al menos el 60% de la población) y la regla de votación aprobada en la cumbre de Bruselas (al menos 15 naciones con al menos el 65% de la población y con 4 o más naciones para formar una coalición de bloqueo).
Tabla 4. Poder de Banzhaf de los 25 miembros de la Unión Europea y 2 candidatos
| EU 27 | Población | Niza | 14 & 60% | 15 & 65% & B |
| Alemania | 17,047 | 7,7828 | 12,761 | 11,869 |
| Francia | 12,316 | 7,7827 | 9,0943 | 8,7366 |
| Reino Unido | 12,254 | 7,7827 | 9,0484 | 8,6919 |
| Italia | 11,839 | 7,7827 | 8,7807 | 8,4359 |
| España | 8,582 | 7,4199 | 6,6372 | 6,3742 |
| Polonia | 7,894 | 7,4198 | 6,3174 | 5,8874 |
| Rumania | 4,497 | 4,2591 | 4,0631 | 4,2174 |
| Países Bajos | 3,344 | 3,9740 | 3,3898 | 3,5049 |
| Grecia | 2,276 | 3,6843 | 2,7660 | 2,8800 |
| Portugal | 2,150 | 3,6843 | 2,6884 | 2,8033 |
| Bélgica | 2,139 | 3,6843 | 2,6826 | 2,7975 |
| República Checa | 2,107 | 3,6843 | 2,6645 | 2,7798 |
| Hungría | 2,095 | 3,6843 | 2,6525 | 2,7679 |
| Suecia | 1,847 | 3,0925 | 2,5089 | 2,6268 |
| Austria | 1,666 | 3,0925 | 2,4012 | 2,5208 |
| Bulgaria | 1,621 | 3,0925 | 2,3712 | 2,4914 |
| Dinamarca | 1,112 | 2,1809 | 2,0650 | 2,1908 |
| Eslovaquia | 1,111 | 2,1809 | 2,0650 | 2,1908 |
| Finlandia | 1,075 | 2,1809 | 2,0470 | 2,1730 |
| Irlanda | 0,819 | 2,1809 | 1,8905 | 2,0196 |
| Lituania | 0,715 | 2,1809 | 1,8302 | 1,9603 |
| Letonia | 0,482 | 1,2502 | 1,6856 | 1,8179 |
| Eslovenia | 0,412 | 1,2502 | 1,6436 | 1,7762 |
| Estonia | 0,280 | 1,2502 | 1,5650 | 1,6993 |
| Chipre | 0,148 | 1,2502 | 1,4865 | 1,6217 |
| Luxemburgo | 0,093 | 1,2502 | 1,4503 | 1,5859 |
| Malta | 0,082 | 0,9422 | 1,4444 | 1,5799 |
Gráfico 1. Poder de Banzhaf de los 25 miembros de la UE con tres reglas de votación
Gráfico 2. Poder de Banzhaf de los 25 miembros de la UE y 2 candidatos
En las Tablas 3 y 4, y los correspondientes Gráficos 1 y 2 pueden observarse los frutos de la rebelión protagonizada en la cumbre de Bruselas por los países de menor población. En efecto, los 19 (en el escenario de 25) y los 21 (en el escenario de 27) países europeos pequeños y medianos ganan poder y los 6 países grandes lo pierden con respecto a la regla de votación de la Convención Europea. Además, ganan más los más pequeños (Malta, Luxemburgo, Chipre, Estonia, Eslovenia y Letonia) y pierden más los más grandes (Alemania, Francia, Reino Unido, Italia, España y Polonia). Finalmente, el poder de Letonia, Eslovenia, Estonia, Chipre, Luxemburgo y Malta aumenta con respecto a las reglas de Niza y de la Convención, siendo España y Polonia los únicos países que pierden poder con respecto a Niza y a la propuesta de la Convención Europea.
El índice de poder de Banzhaf mide el poder de cada nación en el seno del Consejo de Ministros de la Unión Europea cuando toma decisiones usando reglas de votación ponderada. Sin embargo, medir el poder decisional de cada ciudadano europeo es más difícil. La razón es que la participación de los ciudadanos en los procesos de decisión en la Unión Europea es un proceso que tiene dos fases. En la primera, votamos a favor de representantes que llevan una decisión colectiva a las instituciones europeas, siendo éstas las que deciden en una segunda fase, asignando un número de votos a cada representante nacional y estableciendo una cuota que debe superarse para aprobar una moción.
El reparto de votos proporcional a la población de un país puede parecer el mejor método para que el voto de cada ciudadano sea igualitario. Sin embargo, esta apreciación es errónea porque los individuos votan a través de un representante, obligado por el voto de un grupo mayoritario de ciudadanos de su país. Por ejemplo, supongamos que el país A tiene 50 millones de votantes y el país B tiene 49 millones y asignamos a los delegados de cada país un voto por cada millón de votantes. Si usamos la regla de la mayoría simple, son suficientes 25 millones mas uno de votantes de A para que el delegado de A use sus 50 votos para aprobar una directiva que obliga a un colectivo total de 99 millones. Entonces, este procedimiento de votación da más poder a los votantes de A y permite que una minoría se imponga a la mayoría.
Lionel Penrose (1946) propuso el siguiente modelo matemático para analizar sistemas de votación este tipo. Consideremos varias asambleas de votantes disjuntas dos a dos y sea N la unión de todas las asambleas. Cada asamblea tiene un sistema de votación en el que cada votante dispone de un voto y la cuota fijada es la mayoría absoluta. Además, suponemos que cada delegado de una asamblea vota a favor de una propuesta si la mayoría de los votantes de su asamblea la han apoyado y se opone en otro caso. Un razonamiento matemático riguroso, que emplea la fórmula de aproximación de Stirling, permite deducir que el índice de Banzhaf probabilístico de un votante en su asamblea es inversamente proporcional a la raíz cuadrada del número de votantes de su asamblea, siempre que dicho número sea suficientemente grande. Felsenthal y Machover (1998) han demostrado que el poder de un votante de N es igualitario si el índice probabilístico de Banzhaf correspondiente a su delegado es proporcional a la raíz cuadrada del número de votantes de su asamblea.
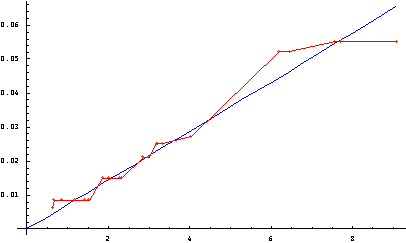
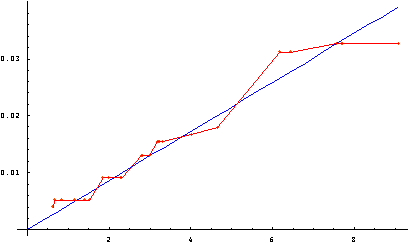
A continuación se exponen los Gráficos 3 y 4, que representan datos bidimensionales. La primera componente, con valores en el eje horizontal, es la raíz cuadrada de la población y la segunda componente, con valores en el eje vertical, es el índice probabilístico de Banzhaf con la regla de Niza. Los gráficos corresponden a los escenarios de 25 y 27 países, respectivamente. Con estos datos se han calculado las funciones lineales de regresión cuyas gráficas son rectas. En los puntos de dichas rectas, el poder es igualitario. Dado que los puntos de cada recta representan una distribución equitativa del poder, concluimos que los ciudadanos de Alemania (el punto situado más a la derecha) tienen menos poder porque está situada debajo de la recta; Francia, el Reino Unido e Italia están en la recta; mientras que España y Polonia se encuentran por encima de ella. El resto de los países oscila en torno a la recta de la igualdad de poder.
Gráfico 3. Poder de los ciudadanos de los 25 países con la regla de Niza
Gráfico 4. Poder de los ciudadanos de los 27 países con la regla de Niza
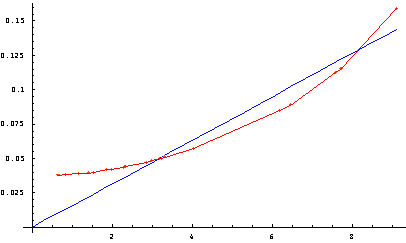
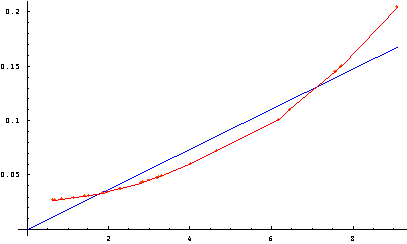
En los Gráficos 5 y 6 se exponen los datos bidimensionales y sus funciones lineales de regresión, datos calculados con la regla de la doble mayoría (al menos 15 naciones con al menos el 65% de la población y con 4 o más naciones para bloquear) aprobada en la cumbre de Bruselas por el Consejo Europeo, para los escenarios de 25 y 27 países. En el escenario de 25 países podemos apreciar el incremento de poder de los alemanes, las pérdidas de franceses, británicos, italianos y holandeses; siendo españoles y polacos quienes sufren el mayor descenso de poder. Analizando el escenario de 27 países, deducimos que la regla de la Constitución aumenta aún más el poder de los alemanes, atribuye un poder superior al igualitario a franceses, británicos, italianos y a los ciudadanos de los seis países menos poblados. Además, esta regla proporciona a los habitantes de los 17 países restantes un poder inferior al reparto equitativo.
Gráfico 5. Poder de los ciudadanos de los 25 países con la regla de la Constitución
Gráfico 6. Poder de los ciudadanos de los 27 países con la regla de la Constitución
Slomczynski y Zyczkowski (2004) han elaborado la regla de votación Penrose-62, que consiste en dar a cada nación un voto proporcional a la raíz cuadrada de su población y establecer una cuota del 62% de la población total. Sus cálculos demuestran que, con la regla P-62, el índice probabilístico de Banzhaf de cada nación europea es casi proporcional a la raíz cuadrada de su población.
Conclusiones: A la vista de estos resultados, un grupo de investigadores en teoría de votación hemos elaborado una carta a los gobiernos de los Estados miembros de la Unión Europea para que se respete el principio democrático básico de que cualquier ciudadano de la Unión Europea tenga el mismo poder de decisión. Debido a que la regla aprobada en Bruselas e incorporada a la Constitución Europea incumple este principio, hemos propuesto que se adopte la regla Penrose-62. Con este sistema de votación lograremos alcanzar la igualdad en el poder decisional de todos los ciudadanos europeos.
Jesús Mario Bilbao Arrese
Catedrático de Matemática Aplicada de la Universidad de Sevilla e investigador de centrA:
Referencias bibliográficas
(1) Algaba, E., J.M. Bilbao, J.R. Fernández y J.J. López (2003), ‘Computing Power Indices in Weighted Multiple Majority Games, Mathematical Social Sciences, 46, pp. 63-80.
(2) Banzhaf III, J.F. (1965), ‘Weighted Voting Doesn’t Work: A Mathematical Analysis’, Rutgers Law Review, 19, pp. 317-343.
(3) Bilbao, J.M., J.R. Fernández y J.J. López (2001), ‘Voting power in the 25-European Union under the Nice Rules’ (Notebook del programa Mathematica), en http://www.esi2.us.es/~mbilbao/notebook/eu25nice.pdf.
(4) Bilbao, J.M., J.R. Fernández y J.J. López (2001), ‘Voting Power in the 27-European Union under the Nice Rules’ (Notebook del programa Mathematica), en http://www.esi2.us.es/~mbilbao/notebook/eu27nice.pdf.
(5) Bilbao, J.M., J.R. Fernández, N. Jiménez y J.J. López (2002), ‘Voting Power in the European Union Enlargement’, European Journal of Operational Research, 143, pp. 181-196.
(6) Dubey, P. y L.S. Shapley (1979), ‘Mathematical Properties of the Banzhaf Power Index’, Mathematics of Operations Research, 4, pp. 99-131.
(7) Felsenthal, D.S. y M. Machover (1998), The Measurement of Voting Power: Theory and Practice, Problems and Paradoxes, Edward Elgar, Cheltenham.
(8) Slomczynski, W. y K. Zyczkowski (2004), Rules Governing Voting in the EU Council, Preprint.